Difference between revisions of "Closure of unit fractions"

From timescalewiki
Jump to: navigation, search
 
(3 intermediate revisions by the same user not shown)
Line 4: Line 4:
  
 
{| class="wikitable"
 
{| class="wikitable"
−
|+$\mathbb{T}= \overline{\left\{\dfrac{1}{n} \colon n \in \mathbb{Z}^+\right\}} $
+
|+$\mathbb{T}=\overline{\left\{\dfrac{1}{n} \colon n \in \mathbb{Z}^+\right\}}$
 
|-
 
|-
−
|Generic element $t\in \mathbb{T}$:
+
|[[Forward jump]]:
−
| Either $t=0$ or for some $n \in \mathbb{Z}^+, t = \dfrac{1}{n}$
+
|$\sigma(t)=\left\{ \begin{array}{ll}
 +
0 &; t=0 \\
 +
\dfrac{1}{k-1} &; t=\dfrac{1}{k}, \quad k \in \{2,3,\ldots\}
 +
\end{array} \right.$
 +
|[[Derivation of forward jump for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Forward graininess]]:
 +
|$\mu(t)=$
 +
|[[Derivation of forward graininess for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Backward jump]]:
 +
|$\rho(t)=$
 +
|[[Derivation of backward jump for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Backward graininess]]:
 +
|$\nu(t)=$
 +
|[[Derivation of backward graininess for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Delta derivative | $\Delta$-derivative]]
 +
|$f^{\Delta}(t)=$
 +
|[[Derivation of delta derivative for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Nabla derivative | $\nabla$-derivative]]
 +
|$f^{\nabla}(t)=$
 +
|[[Derivation of nabla derivative for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Delta integral | $\Delta$-integral]]
 +
|$\displaystyle\int_s^t f(\tau) \Delta \tau=$
 +
|[[Derivation of delta integral for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Nabla integral | $\nabla$-integral]]
 +
|$\displaystyle\int_s^t f(\tau) \nabla \tau=$
 +
|[[Derivation of nabla integral for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Delta hk|$h_k(t,s)$]]
 +
|$h_k(t,s)=$
 +
|[[Derivation of delta hk for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Nabla hk|$\hat{h}_k(t,s)$]]
 +
|$\hat{h}_k(t,s)=$
 +
|[[Derivation of nabla hk for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Delta gk|$g_k(t,s)$]]
 +
|$g_k(t,s)=$
 +
|[[Derivation of delta gk for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Nabla gk|$\hat{g}_k(t,s)$]]
 +
|$\hat{g}_k(t,s)=$
 +
|[[Derivation of nabla gk for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Delta exponential | $e_p(t,s)$]]
 +
|$e_p(t,s)=$
 +
|[[Derivation of delta exponential T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Nabla exponential | $\hat{e}_p(t,s)$]]
 +
|$\hat{e}_p(t,s)=$
 +
|[[Derivation of nabla exponential T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Gaussian bell]]
 +
|$\mathbf{E}(t)=$
 +
|[[Derivation of Gaussian bell for T=Closure of unit fractions|derivation]]
 
|-
 
|-
−
|Jump operator:
+
|[[Delta sine | $\mathrm{sin}_p(t,s)=$]]
−
|$\sigma(t) = \left\{ \begin{array}{ll}
+
|$\sin_p(t,s)=$
−
\dfrac{1-t}{t} &; t>1 \\
+
|[[Derivation of delta sin sub p for T=Closure of unit fractions|derivation]]
−
0 &; t=0
+
|-
−
\end{array} \right.$
+
|$\mathrm{\sin}_1(t,s)$
 +
|$\sin_1(t,s)=$
 +
|[[Derivation of delta sin sub 1 for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Nabla sine|$\widehat{\sin}_p(t,s)$]]
 +
|$\widehat{\sin}_p(t,s)=$
 +
|[[Derivation of nabla sine sub p for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Delta cosine|$\mathrm{\cos}_p(t,s)$]]
 +
|$\cos_p(t,s)=$
 +
|[[Derivation of delta cos sub p for T=Closure of unit fractions|derivation]]
 +
|-
 +
|$\mathrm{\cos}_1(t,s)$
 +
|$\cos_1(t,s)=$
 +
|[[Derivation of delta cos sub 1 for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Nabla cosine|$\widehat{\cos}_p(t,s)$]]
 +
|$\widehat{\cos}_p(t,s)=$
 +
|[[Derivation of nabla cos sub 1 for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Delta sinh|$\sinh_p(t,s)$]]
 +
|$\sinh_p(t,s)=$
 +
|[[Derivation of delta sinh sub p for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Nabla sinh|$\widehat{\sinh}_p(t,s)$]]
 +
|$\widehat{\sinh}_p(t,s)=$
 +
|[[Derivation of nabla sinh sub p for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Delta cosh|$\cosh_p(t,s)$]]
 +
|$\cosh_p(t,s)=$
 +
|[[Derivation of delta cosh sub p for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Nabla cosh|$\widehat{\cosh}_p(t,s)$]]
 +
|$\widehat{\cosh}_p(t,s)=$
 +
|[[Derivation of nabla cosh sub p for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Gamma function]]
 +
|$\Gamma_{\overline{\left\{\frac{1}{n} \colon n \in \mathbb{Z}^+\right\}}}(x,s)=$
 +
|[[Derivation of gamma function for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Euler-Cauchy logarithm]]
 +
|$L(t,s)=$
 +
|[[Derivation of Euler-Cauchy logarithm for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Bohner logarithm]]
 +
|$L_p(t,s)=$
 +
|[[Derivation of the Bohner logarithm for T=Closure of unit fractions|derivation]]
 +
|-
 +
|[[Jackson logarithm]]
 +
|$\log_{\overline{\left\{\frac{1}{n} \colon n \in \mathbb{Z}^+\right\}}} g(t)=$
 +
|[[Derivation of the Jackson logarithm for T=Closure of unit fractions|derivation]]
 
|-
 
|-
−
|Graininess operator:
+
|[[Mozyrska-Torres logarithm]]
−
|$\mu(t) = \left\{ \begin{array}{ll}
+
|$L_{\overline{\left\{\frac{1}{n} \colon n \in \mathbb{Z}^+\right\}}}(t)=$
−
\dfrac{1-t-t^2}{t} &; t>0 \\
+
|[[Derivation of the Mozyrska-Torres logarithm for T=Closure of unit fractions|derivation]]
−
0 &; t=0
 
−
\end{array} \right.$
 
 
|-
 
|-
−
|[[Delta_derivative | $\Delta$-derivative:]]
+
|[[Laplace transform]]
−
|$f^{\Delta}(t) = \left\{ \begin{array}{ll}
+
|$\mathscr{L}_{\overline{\left\{\frac{1}{n} \colon n \in \mathbb{Z}^+\right\}}}\{f\}(z;s)=$
−
\dfrac{t}{1-t} \left[ f \left(\dfrac{1-t}{t} \right)-f(t) \right] &; t>0 \\
+
|[[Derivation of Laplace transform for T=Closure of unit fractions|derivation]]
−
\displaystyle\lim_{h \rightarrow 0} \dfrac{f(h)-f(0)}{h} &; t=0
 
−
\end{array} \right.$
 
 
|-
 
|-
−
|[[Delta_integral | $\Delta$-integral:]]
+
|[[Hilger circle]]  
−
|  
+
|
 +
|[[Derivation of Hilger circle for T=Closure of unit fractions|derivation]]
 
|-
 
|-
−
|[[Exponential_functions | Exponential function]]:
 
−
|
 
 
|}
 
|}
 +
  
 
<center>{{:Time scales footer}}</center>
 
<center>{{:Time scales footer}}</center>

Latest revision as of 22:32, 23 February 2016

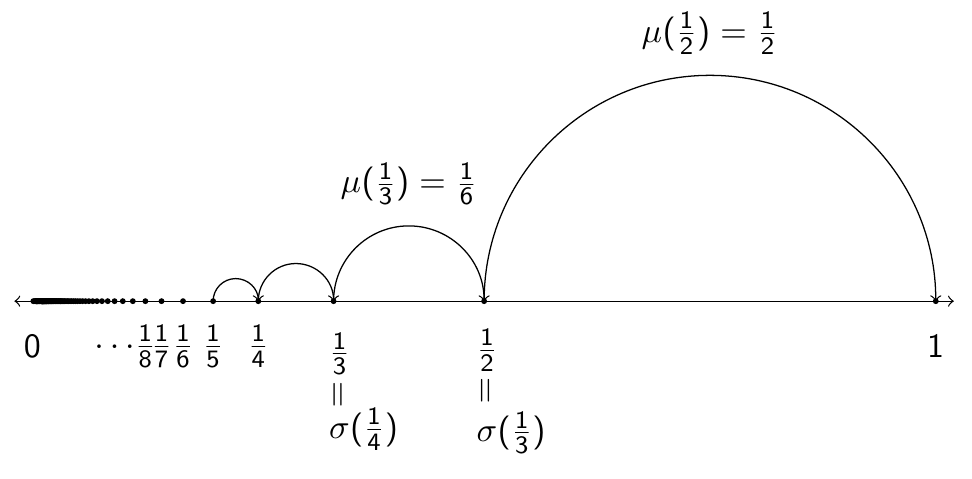
The set $\overline{\left\{\dfrac{1}{n} \colon n \in \mathbb{Z}^+\right\}}=\left\{ 0,1,\dfrac{1}{2},\dfrac{1}{3},\ldots \right\}$, where the $\overline{\mathrm{overline}}$ denotes topological closure of this set in the usual topology on $\mathbb{R}$ is a time scale.

Closureunitfractionstimescale.png

$\mathbb{T}=\overline{\left\{\dfrac{1}{n} \colon n \in \mathbb{Z}^+\right\}}$
Forward jump: $\sigma(t)=\left\{ \begin{array}{ll} 0 &; t=0 \\ \dfrac{1}{k-1} &; t=\dfrac{1}{k}, \quad k \in \{2,3,\ldots\} \end{array} \right.$ derivation
Forward graininess: $\mu(t)=$ derivation
Backward jump: $\rho(t)=$ derivation
Backward graininess: $\nu(t)=$ derivation
$\Delta$-derivative $f^{\Delta}(t)=$ derivation
$\nabla$-derivative $f^{\nabla}(t)=$ derivation
$\Delta$-integral $\displaystyle\int_s^t f(\tau) \Delta \tau=$ derivation
$\nabla$-integral $\displaystyle\int_s^t f(\tau) \nabla \tau=$ derivation
$h_k(t,s)$ $h_k(t,s)=$ derivation
$\hat{h}_k(t,s)$ $\hat{h}_k(t,s)=$ derivation
$g_k(t,s)$ $g_k(t,s)=$ derivation
$\hat{g}_k(t,s)$ $\hat{g}_k(t,s)=$ derivation
$e_p(t,s)$ $e_p(t,s)=$ derivation
$\hat{e}_p(t,s)$ $\hat{e}_p(t,s)=$ derivation
Gaussian bell $\mathbf{E}(t)=$ derivation
$\mathrm{sin}_p(t,s)=$ $\sin_p(t,s)=$ derivation
$\mathrm{\sin}_1(t,s)$ $\sin_1(t,s)=$ derivation
$\widehat{\sin}_p(t,s)$ $\widehat{\sin}_p(t,s)=$ derivation
$\mathrm{\cos}_p(t,s)$ $\cos_p(t,s)=$ derivation
$\mathrm{\cos}_1(t,s)$ $\cos_1(t,s)=$ derivation
$\widehat{\cos}_p(t,s)$ $\widehat{\cos}_p(t,s)=$ derivation
$\sinh_p(t,s)$ $\sinh_p(t,s)=$ derivation
$\widehat{\sinh}_p(t,s)$ $\widehat{\sinh}_p(t,s)=$ derivation
$\cosh_p(t,s)$ $\cosh_p(t,s)=$ derivation
$\widehat{\cosh}_p(t,s)$ $\widehat{\cosh}_p(t,s)=$ derivation
Gamma function $\Gamma_{\overline{\left\{\frac{1}{n} \colon n \in \mathbb{Z}^+\right\}}}(x,s)=$ derivation
Euler-Cauchy logarithm $L(t,s)=$ derivation
Bohner logarithm $L_p(t,s)=$ derivation
Jackson logarithm $\log_{\overline{\left\{\frac{1}{n} \colon n \in \mathbb{Z}^+\right\}}} g(t)=$ derivation
Mozyrska-Torres logarithm $L_{\overline{\left\{\frac{1}{n} \colon n \in \mathbb{Z}^+\right\}}}(t)=$ derivation
Laplace transform $\mathscr{L}_{\overline{\left\{\frac{1}{n} \colon n \in \mathbb{Z}^+\right\}}}\{f\}(z;s)=$ derivation
Hilger circle derivation


Examples of time scales
$\Huge\mathbb{R}$
Real numbers
$\Huge\mathbb{Z}$
Integers
$\Huge{h\mathbb{Z}}$
Multiples of integers
$\Huge\mathbb{Z}^2$
Square integers
$\Huge\mathbb{H}$
Harmonic numbers
$\Huge\mathbb{T}_{\mathrm{iso}}$
Isolated points
$\Huge\sqrt[n]{\mathbb{N}_0}$
nth root numbers
$\Huge\mathbb{P}_{a,b}$
Evenly spaced intervals
$\huge\overline{q^{\mathbb{Z}}}$
Quantum, $q>1$
$\huge\overline{q^{\mathbb{Z}}}$
Quantum, $q<1$
$\overline{\left\{\dfrac{1}{n} \colon n \in \mathbb{Z}^+\right\}}$
Closure of unit fractions
$\Huge\mathcal{C}$
Cantor set
Retrieved from "http://timescalewiki.org/index.php?title=Closure_of_unit_fractions&oldid=1042"