Integers

The set $\mathbb{Z}=\{\ldots,-2,-1,0,1,2,\ldots\}$ of integers is a time scale.

$\mathbb{T}=\mathbb{Z}$

Generic element $t\in \mathbb{T}$	For some $n \in \mathbb{Z}, t =n$
Jump operator	$\sigma(t)=t+1$
Graininess operator	$\mu(t)=1$
$\Delta$-derivative	$f^{\Delta}(t)=f(t+1)-f(t)$
$\nabla$-derivative	$f^{\nabla}(t)=f(t)-f(t-1)$
$\Delta$-integral	$$\int_s^t f(\tau) \Delta \tau = \left\{ \begin{array}{ll} \sum_{k=s}^{t-1} f(k) &; t > s \\ 0 &; t=s \\ -\sum_{k=t}^{s-1} f(k) &; t < s \end{array} \right.$$
$\nabla$-integral	$$\int_s^t f(\tau) \nabla \tau = \left\{ \begin{array}{ll} \displaystyle\sum_{k=s+1}^t f(k) &; t>s \\ 0 &; t=s \\ -\sum_{k=t+1}^s f(k) &; t<s \end{array} \right.$$
$\Delta$-exponential	$\begin{array}{ll} e_p(t,s) &= \exp \left( \displaystyle\int_{s}^{t} \dfrac{1}{\mu(\tau)} \log(1 + p(\tau)) \Delta \tau \right) \\ &= \exp \left( \displaystyle\sum_{k=s}^{t-1} \log(1+p(k)) \right) \\ &= \displaystyle\prod_{k=s}^{t-1} \left( 1+p(k) \right) \\ \end{array}$
$\mathrm{sin}_p(t,0)$	$$\begin{array}{ll} \sin_p(t,t_0) &= \dfrac{e_{ip}(t,t_0)-e_{-ip}(t,t_0)}{2i} \\ &= \dfrac{\displaystyle\prod_{k=t_0}^{t-1}1+ip(k) - \displaystyle\prod_{k=t_0}^{t-1}1-ip(k)}{2i} \end{array}$$
$\mathrm{sin}_1(t,0)$	$$\begin{array}{ll} \sin_1(t,0) &= \dfrac{(1+i)^{t}-(1-i)^{t}}{2i} \\ &= \dfrac{\displaystyle\sum_{k=0}^{t} {t \choose k} i^k - \displaystyle\sum_{k=0}^{t} (-1)^k {t \choose k} i^k}{2i} \end{array}$$
$\mathrm{cos}_p(t,t_0)$	$$\begin{array}{ll} \cos_p(t,t_0) &= \dfrac{e_{ip}(t,t_0)+e_{-ip}(t,t_0)}{2} \\ &= \dfrac{\displaystyle\prod_{k=t_0}^{t-1}1+ip(k) + \displaystyle\prod_{k=t_0}^{t-1}1-ip(k)}{2} \end{array}$$
$\mathrm{cos}_1(t,0)$	\begin{array}{ll} \cos_1(t,0) &= \dfrac{(1+i)^{t}+(1-i)^{t}}{2} \\ &= \dfrac{\displaystyle\sum_{k=0}^{t} {t \choose k} i^k + \displaystyle\sum_{k=0}^{t} (-1)^k {t \choose k} i^k}{2} \end{array}
Hilger circle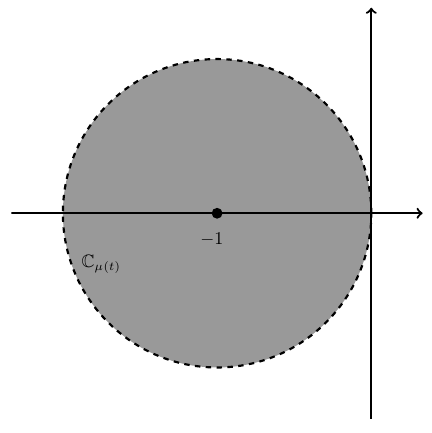
Gamma function:	$\Gamma_{\mathbb{Z}}(t;s)=\displaystyle\sum_{k=0}^{\infty} \left( \displaystyle\prod_{j=s}^{k-1} \dfrac{j+x}{j+1} \right) \dfrac{1}{2^{k+1}}$