Delta gk

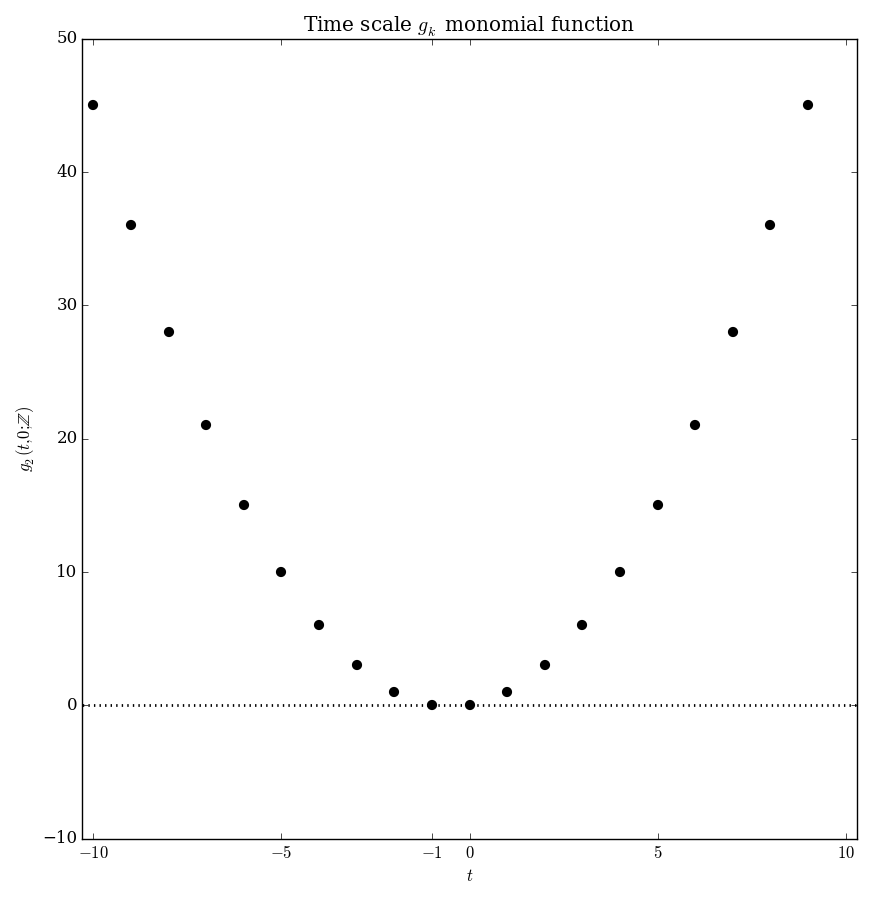
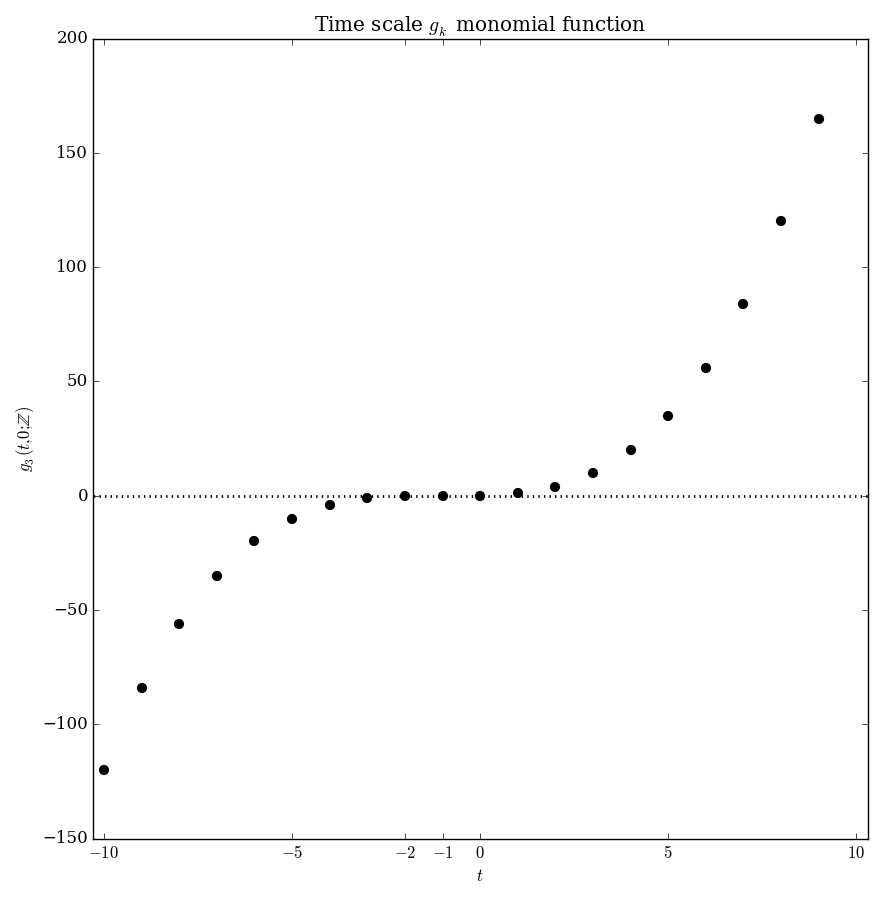
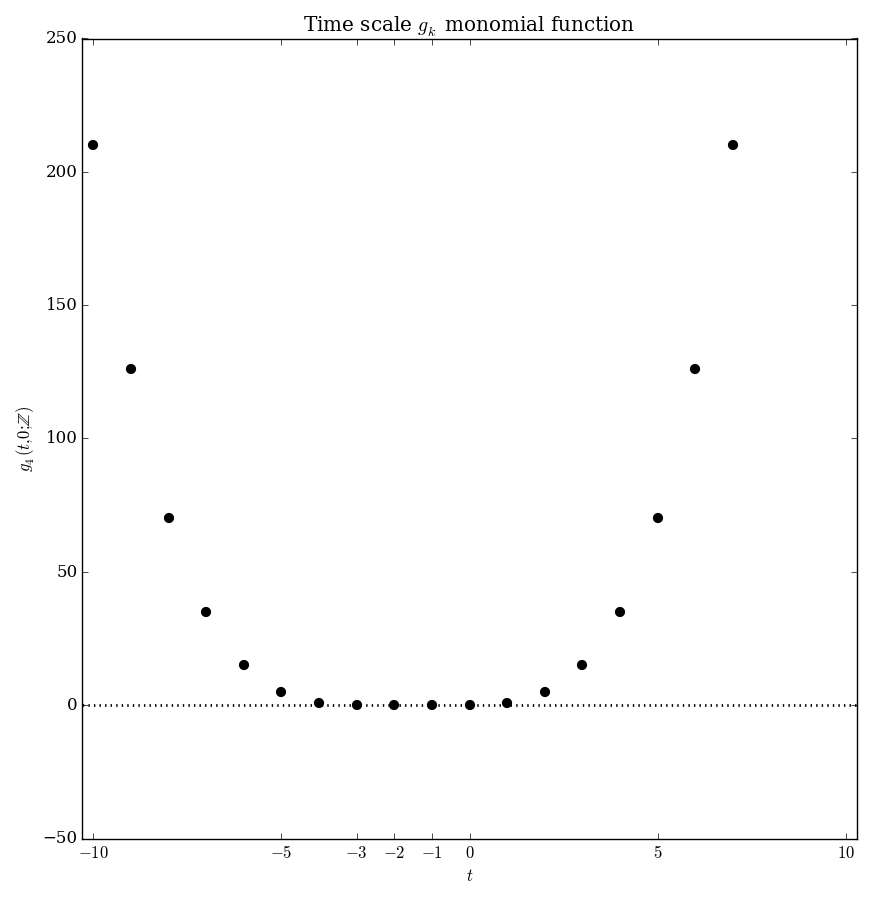
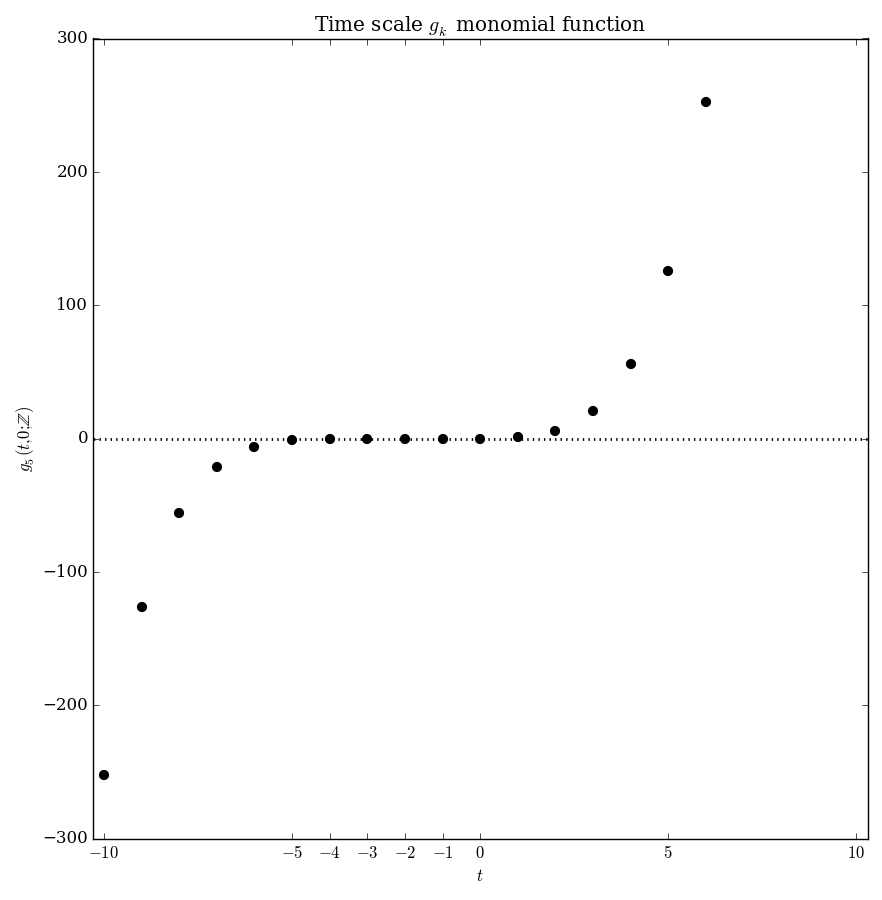
Let $\mathbb{T}$ be a time scale and let $t,s \in \mathbb{T}$. The $g_k$ monomials are defined by the recurrence $$\left\{ \begin{array}{ll} g_0(t,s)=1 \\ g_{k+1}(t,s)=\displaystyle\int_s^t g_k(\sigma(\tau),s) \Delta \tau. \end{array} \right.$$

• 

  Graph of $g_2(t,0;\mathbb{Z})$.

• 

  Graph of $g_3(t,0;\mathbb{Z})$.

• 

  Graph of $g_4(t,0;\mathbb{Z})$.

• 

  Graph of $g_5(t,0;\mathbb{Z})$.

Properties

Zeros of delta gk
Relationship between delta hk and delta gk

Examples

Delta $g_k$ Monomials

$\mathbb{T}=$	$g_k(t,t_0)=$
$\mathbb{R}$	$g_k(t,t_0)=\dfrac{(t-t_0)^k}{k!}$
$\mathbb{Z}$	$g_k(t,t_0)= $
$h\mathbb{Z}$	$g_k(t,t_0)=$
$\mathbb{Z}^2$	$g_k(t,t_0)=$
$\overline{q^{\mathbb{Z}}}, q > 1$	$g_k(t,t_0)=$
$\overline{q^{\mathbb{Z}}}, q < 1$	$g_k(t,t_0)=$
$\mathbb{H}$	$g_k(t,t_0)=$

See also

Delta hk

$\Delta$-special functions on time scales
$\cos_p$	$\cosh_p$	$e_p$	$g_k$	$h_k$	$\sin_p$	$\sinh_p$