Difference between revisions of "Delta exponential"
(→See Also) |
|||
| Line 103: | Line 103: | ||
[[Category:specialfunction]] | [[Category:specialfunction]] | ||
| + | [[Category:Definition]] | ||
Latest revision as of 14:12, 28 January 2023
Let $\mathbb{T}$ be a time scale. Let $p \in \mathcal{R}(\mathbb{T},\mathbb{C})$ be a regressive function. The $\Delta$-exponential function $e_p (\cdot,\cdot;\mathbb{T}) \colon \mathbb{T} \times \mathbb{T} \rightarrow \mathbb{R}$ is defined by the formula $$e_p(t,s;\mathbb{T}) = \exp \left( \displaystyle\int_s^t \xi_{\mu(\tau)}(p(\tau))\Delta \tau \right),$$ where $\exp$ denotes the exponential function and $\xi_{\mu(\tau)}$ denotes the cylinder transformation.
Graph of $e_2(t,-1;\mathbb{Z})$.
Graph of $e_2(t,0;\mathbb{Z})$.
Graph of $e_2(t,1;\mathbb{Z})$.
Properties
Delta exponential dynamic equation
Semigroup property of delta exponential
Delta exponential with p=0
Delta exponential with t=s
Delta simple useful formula
Reciprocal of delta exponential
Product of delta exponentials with fixed t and s
Quotient of delta exponentials with fixed t and s
Relationship between delta exponential and nabla exponential
Relationship between delta exponential and nabla exponential
Relationship between nabla exponential and delta exponential
Proposition: The following formula holds: $$e_{\ominus z}(\sigma(t),s) = \dfrac{e_{\ominus z}(t,s)}{1+\mu(t)z} = -\dfrac{(\ominus z)(t)}{z} e_{\ominus z}(t,s).$$
Examples
| $\mathbb{T}=$ | $e_p(t,s)=$ |
| $\mathbb{R}$ | $e_p(t,s)= \left\{ \begin{array}{ll} \exp \left( \displaystyle\int_s^t p(\tau) d \tau \right) &; t>s \\ 1 &; t=s \\ \exp \left( -\displaystyle\int_t^s p(\tau) d\tau \right) &; t<s \end{array} \right.$ |
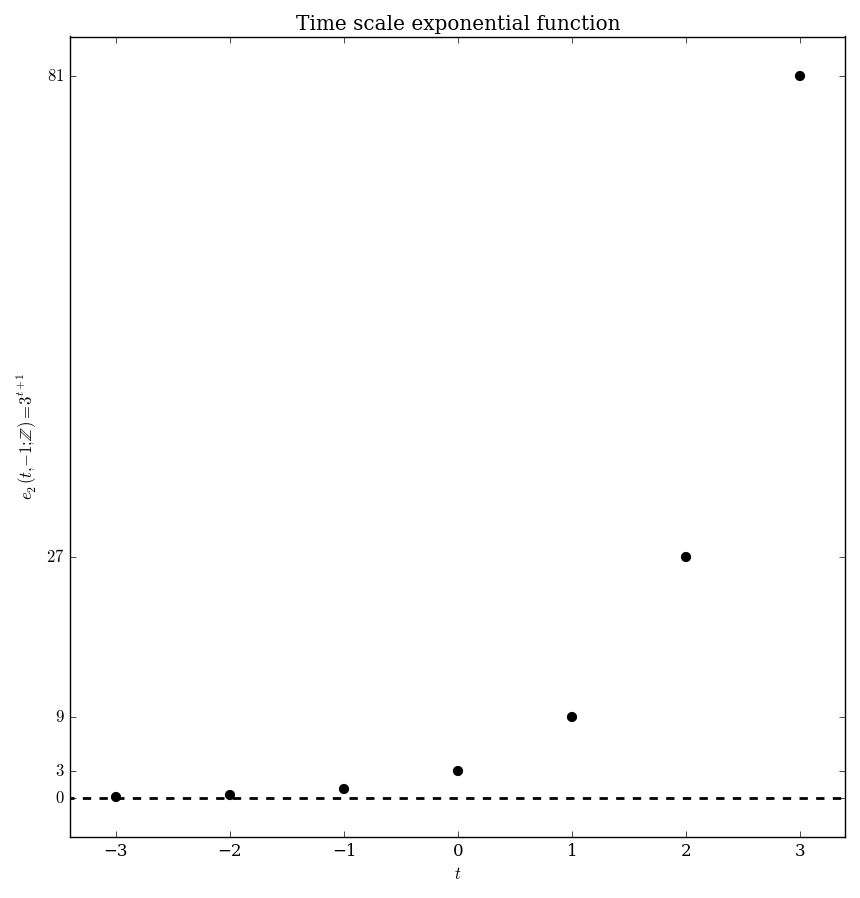
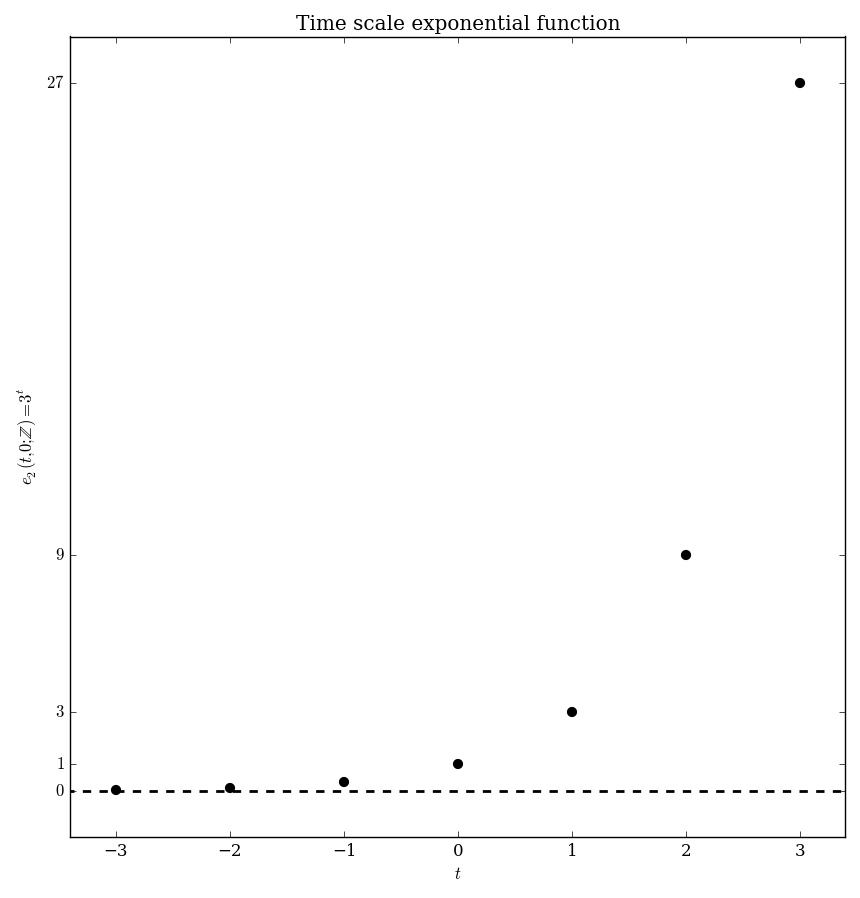
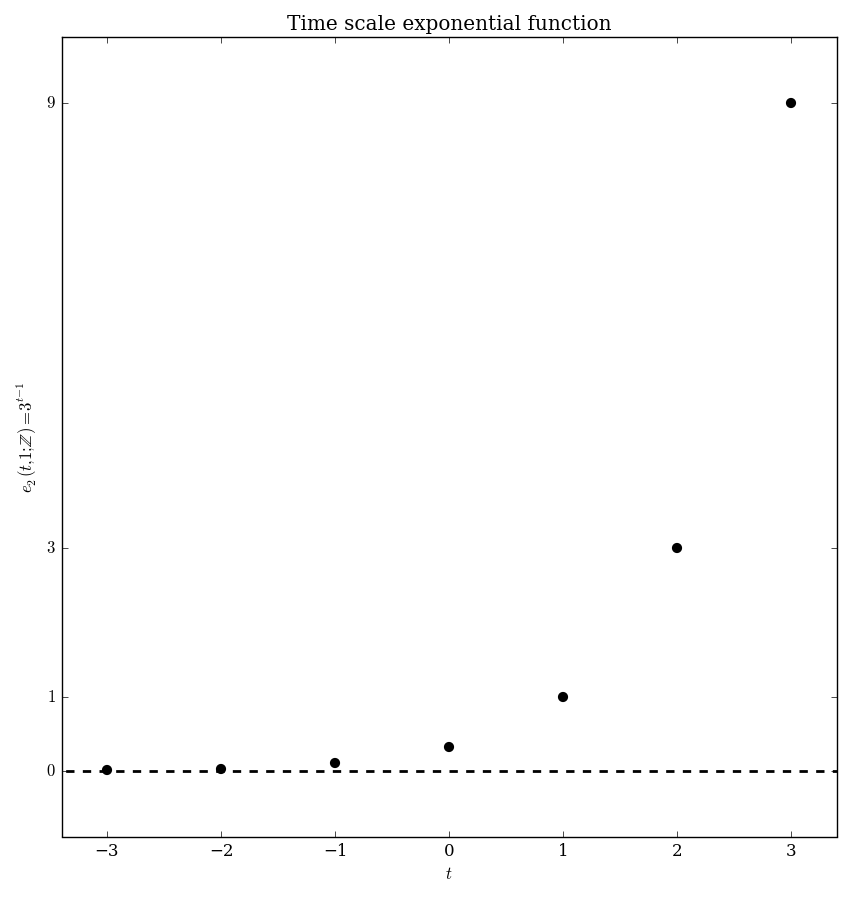
| $\mathbb{Z}$ | $e_p(t,s) = \left\{ \begin{array}{ll} \displaystyle\prod_{k=s}^{t-1} 1+p(k) &; t > s \\ 1 &; t=s \\ \displaystyle\prod_{k=t}^{s-1} \dfrac{1}{1+p(k)}&; t < s \end{array} \right.$ |
| $h\mathbb{Z}$ | $ e_p(t,s) = \left\{ \begin{array}{ll} \displaystyle\prod_{k=\frac{s}{h}}^{\frac{t}{h}-1} (1+hp(hk)) &; t > s \\ 1 &; t=s \\ \displaystyle\prod_{k=\frac{t}{h}}^{\frac{s}{h}-1} \dfrac{1}{1+hp(hk)} &; t < s \end{array} \right.$ |
| $\mathbb{Z}^2$ | $ e_p(t,s) = \left\{\begin{array}{ll} \displaystyle\prod_{k=\sqrt{s}}^{\sqrt{t}-1} 1 + p(k^2)(2k+1) &; t > s \\ 1 &; t=s\\ \displaystyle\prod_{k=\sqrt{t}}^{\sqrt{s}-1} \dfrac{1}{1+p(k^2)(2k+1)} &; t < s \end{array} \right.$ |
| $\overline{q^{\mathbb{Z}}}, q > 1$ | $e_p(t,s) = \left\{ \begin{array}{ll} \displaystyle\prod_{k=\log_q(s)}^{\log_q(t)-1} 1 + p(q^k)q^k(q-1) &; t > s \\ 1 &; t=s \\ \displaystyle\prod_{k=\log_q(t)}^{\log_q(s)-1} \dfrac{1}{1+p(q^k)q^k(q-1)} &; t < s \end{array} \right.$ |
| $\overline{q^{\mathbb{Z}}}, q < 1$ | $e_p(t,s) = \left\{ \begin{array}{ll} \displaystyle\prod_{k=\log_q(s)}^{\log_q(t)-1} 1 + p(q^k)q^{k-1}(1-q) &; t > s \\ 1 &; t=s \\ \displaystyle\prod_{k=\log_q(t)}^{\log_q(s)-1} \dfrac{1}{1+p(q^k)q^{k-1}(1-q)} &; t < s \end{array} \right.$ |
| $\mathbb{H}$ | $ e_p(t,s) = e_p\left( \displaystyle\sum_{k=1}^n \dfrac{1}{k}, \displaystyle\sum_{k=1}^m \dfrac{1}{k} \right) = \left\{\begin{array}{ll} \displaystyle\prod_{k=m}^{n-1} {1 + \dfrac{1}{k+1} p \left( \displaystyle\sum_{j=1}^k \dfrac{1}{j} \right)} &; t > s \\ 1 &; t=s \\ \displaystyle\prod_{k=n}^{m-1} \dfrac{1}{1 + \dfrac{1}{k+1} p \left( \displaystyle\sum_{j=1}^k \dfrac{1}{j} \right)} &; t < s \end{array} \right.$ |
See Also
Nabla exponential
Gaussian bell
References
- Martin Bohner and Allan Peterson: Dynamic Equations on Time Scales (2001)... (previous)... (next): Definition $2.30$
$\Delta$-special functions on time scales | ||||||
 $\cos_p$ |
 $\cosh_p$ |
 $e_p$ |
 $g_k$ |
 $h_k$ |
 $\sin_p$ |
 $\sinh_p$ |
