Difference between revisions of "Delta cosine"
| Line 21: | Line 21: | ||
=See Also= | =See Also= | ||
[[Delta cosine]] <br /> | [[Delta cosine]] <br /> | ||
| − | [[Delta | + | [[Delta cosh]]<br /> |
<center>{{:Delta special functions footer}}</center> | <center>{{:Delta special functions footer}}</center> | ||
Revision as of 22:32, 2 June 2016
Let $\mathbb{T}$ be a time scale and let $t_0 \in \mathbb{T}$ and let $\mu p^2 \colon \mathbb{T} \rightarrow \mathbb{R}$ be a regressive function. We define the trigonometric functions $\cos_p \colon \mathbb{T} \rightarrow \mathbb{R}$ $$\cos_p(t,t_0)=\dfrac{e_{ip}(t,t_0)+e_{-ip}(t,t_0)}{2},$$ where $i=\sqrt{-1}$.
Contents
Properties
Theorem
The following formula holds: $$\cos_p^{\Delta}(t,t_0)=-p(t)\sin_p(t,t_0),$$ where $\cos^{\Delta}_p$ denotes the delta derivative of the delta cosine function and $\sin_p$ denotes the delta sine function.
Proof
Compute $$\begin{array}{ll} \cos_p^{\Delta}(t,t_0) &= \dfrac{1}{2} \dfrac{\Delta}{\Delta t} \Big(e_{ip}(t,t_0) + e_{-ip}(t,t_0) \Big) \\ &= \dfrac{ip}{2} (e_{ip}-e_{-ip}(t,t_0)) \\ &= -\dfrac{p}{2i} (e_{ip}-e_{-ip}(t,t_0)) \\ &= -\sin_p(t,t_0), \end{array}$$ as was to be shown. █
References
Theorem
The following formula holds: $$\cos_p^2(t,t_0)+\sin_p^2(t,t_0)=e_{\mu p^2}(t,t_0),$$ where $\cos_p$ denotes the $\Delta$-$\cos_p$ function and $\sin_p$ denotes the $\Delta$-$\sin_p$ function.
Proof
References
Relation to other special functions
Theorem
The following formula holds: $$\sin_p^{\Delta}(t,t_0)=p(t)\cos_p(t,t_0),$$ where $\sin_p$ denotes the $\Delta$-$\sin_p$ function and $\cos_p$ denotes the $\Delta$-$\cos_p$ function.
Proof
Compute $$\begin{array}{ll} \sin^{\Delta}_p(t,t_0) &= \dfrac{1}{2i} \dfrac{\Delta}{\Delta t} \left( e_{ip}(t,t_0) - e_{-ip}(t,t_0) \right) \\ &= \dfrac{ip}{2i} ( e_{ip}(t,t_0) + e_{-ip}(t,t_0) ) \\ &= \dfrac{1}{2} (e_{ip}(t,t_0)+e_{-ip}(t,t_0)) \\ &= p\cos_p(t,t_0), \end{array}$$ as was to be shown. █
References
Examples
| $\mathbb{T}$ | $\cos_p(t,s)= $ |
| $\mathbb{R}$ | |
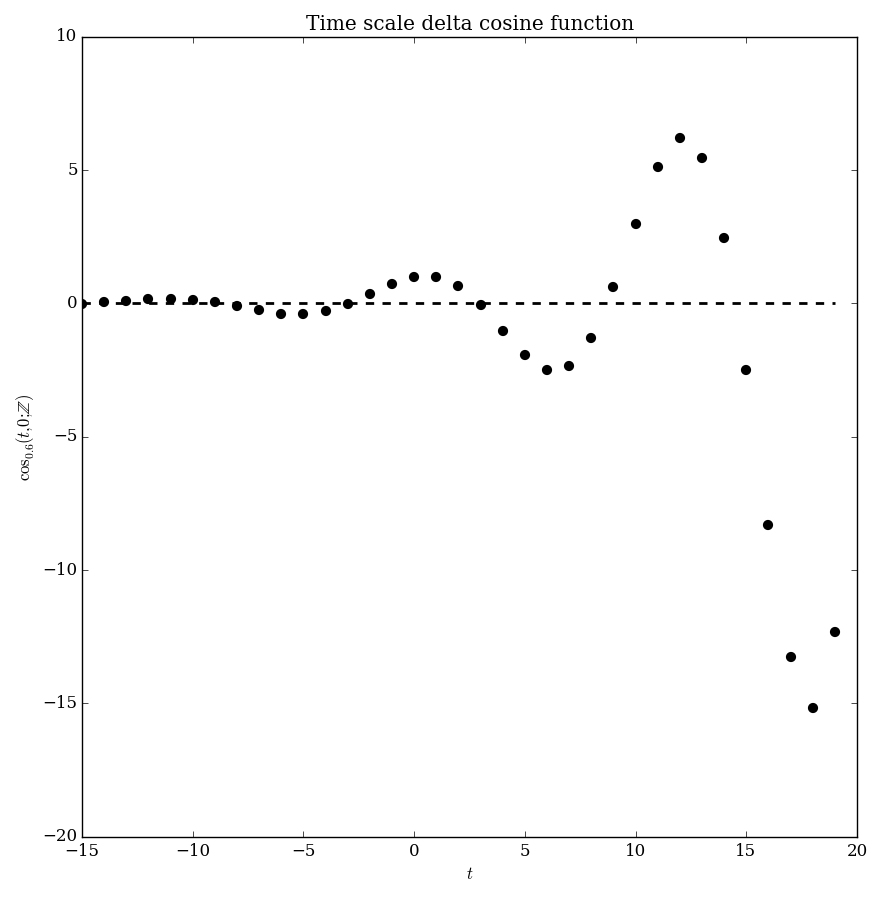
| $\mathbb{Z}$ | |
| $h\mathbb{Z}$ | |
| $\mathbb{Z}^2$ | |
| $\overline{q^{\mathbb{Z}}}, q > 1$ | |
| $\overline{q^{\mathbb{Z}}}, q < 1$ | |
| $\mathbb{H}$ |
See Also
Delta cosine
Delta cosh
$\Delta$-special functions on time scales | ||||||
$\cos_p$ |
$\cosh_p$ |
$e_p$ |
$g_k$ |
$h_k$ |
$\sin_p$ |
$\sinh_p$ |