Difference between revisions of "Delta exponential"
| Line 1: | Line 1: | ||
| − | Let $\mathbb{T}$ be a [[time scale]]. Define $\xi_h(z) := \dfrac{1}{h} \log(1+zh)$. Let $p \in \mathcal{R}(\mathbb{T},\mathbb{ | + | Let $\mathbb{T}$ be a [[time scale]]. Define $\xi_h(z) := \dfrac{1}{h} \log(1+zh)$. Let $p \in \mathcal{R}(\mathbb{T},\mathbb{C})$ be a [[regressive_function | regressive function]]. The $\Delta$-exponential function $e_p (\cdot,\cdot;\mathbb{T}) \colon \mathbb{T} \times \mathbb{T} \rightarrow \mathbb{R}$ is defined by the formula |
$$e_p(t,s;\mathbb{T}) = \exp \left( \displaystyle\int_s^t \xi_{\mu(\tau)}(p(\tau))\Delta \tau \right),$$ | $$e_p(t,s;\mathbb{T}) = \exp \left( \displaystyle\int_s^t \xi_{\mu(\tau)}(p(\tau))\Delta \tau \right),$$ | ||
Revision as of 08:07, 1 June 2016
Let $\mathbb{T}$ be a time scale. Define $\xi_h(z) := \dfrac{1}{h} \log(1+zh)$. Let $p \in \mathcal{R}(\mathbb{T},\mathbb{C})$ be a regressive function. The $\Delta$-exponential function $e_p (\cdot,\cdot;\mathbb{T}) \colon \mathbb{T} \times \mathbb{T} \rightarrow \mathbb{R}$ is defined by the formula
$$e_p(t,s;\mathbb{T}) = \exp \left( \displaystyle\int_s^t \xi_{\mu(\tau)}(p(\tau))\Delta \tau \right),$$ where $\exp$ denotes the exponential function. It turns out that $e_p$ is the unique solution to the dynamic initial value problem $$y^{\Delta} = py, \quad y(s)=1.$$
Contents
- 1 Properties
- 1.1 Theorem
- 1.2 Proof
- 1.3 References
- 1.4 Theorem
- 1.5 Proof
- 1.6 References
- 1.7 Theorem
- 1.8 Proof
- 1.9 References
- 1.10 Theorem
- 1.11 Proof
- 1.12 References
- 1.13 Theorem
- 1.14 Proof
- 1.15 References
- 1.16 Theorem
- 1.17 Proof
- 1.18 References
- 1.19 Theorem
- 1.20 Proof
- 1.21 References
- 1.22 Theorem
- 1.23 Proof
- 1.24 References
- 1.25 Theorem
- 1.26 Proof
- 1.27 References
- 1.28 Theorem
- 1.29 Proof
- 1.30 References
- 2 Examples
- 3 See Also
Properties
Theorem
Let $\mathbb{T}$ be a time scale, let $t,s \in \mathbb{T}$, and let $p \in \mathcal{R}\left( \mathbb{T},\mathbb{C} \right)$ be a forward regressive function. The following formula holds for all $s,t \in \mathbb{T}$: $$e_p(t,r;\mathbb{T})e_p(r,s;\mathbb{T})=e_p(t,s;\mathbb{T}),$$ where $e_p$ denotes the delta exponential.
Proof
References
- Martin Bohner and Allan Peterson: Dynamic Equations on Time Scales (2001)... (previous)... (next): Lemma $2.31$
Theorem
Let $\mathbb{T}$ be a time scale and let $t,s \in \mathbb{T}$. Then the following formula holds: $$e_0(t,s;\mathbb{T})=1,$$ where $e_0$ denotes the delta exponential.
Proof
References
Theorem
Let $\mathbb{T}$ be a time scale, let $t \in \mathbb{T}$, and $p \colon \mathbb{T} \rightarrow \mathbb{C}$ a regressive function. The following formula holds: $$e_p(t,t;\mathbb{T})=1,$$ where $e_p$ denotes the delta exponential.
Proof
References
Theorem
Let $\mathbb{T}$ be a time scale, let $t,s \in \mathbb{T}$, and $p \in \mathcal{R} \left( \mathbb{T},\mathbb{C} \right)$ be a regressive function. The following formula holds: $$e_p(\sigma(t),s;\mathbb{T})=(1+\mu(t)p(t))e_p(t,s;\mathbb{T}),$$ where $e_p$ denotes the delta exponential, $\sigma$ denotes the forward jump, and $\mu$ denotes the forward graininess.
Proof
References
- Martin Bohner and Allan Peterson: Dynamic Equations on Time Scales (2001)... (previous)... (next): Theorem 1.16 (iv)
Theorem
Let $\mathbb{T}$ be a time scale, let $t,s \in \mathbb{T}$, and let $p \in \mathcal{R}(\mathbb{T},\mathbb{C})$ be a regressive function. The following formula holds: $$\dfrac{1}{e_p(t,s;\mathbb{T})}=e_{\ominus p}(s,t;\mathbb{T}),$$ where $e_p$ denotes the delta exponential and $\ominus$ denotes circle minus.
Proof
References
Theorem
Let $\mathbb{T}$ be a time scale, $t,s \in \mathbb{T}$, and let $p,q \in \mathcal{R}\left(\mathbb{T},\mathbb{C}\right)$ be regressive functions. The following formula holds: $$e_p(t,s;\mathbb{T})e_q(t,s;\mathbb{T})=e_{p \oplus q}(t,s;\mathbb{T}),$$ where $e_p$ denotes the delta exponential and $\oplus$ denotes circle plus.
Proof
References
Theorem
Let $\mathbb{T}$ be a time scale, $t,s \in \mathbb{T}$, and let $p,q \in \mathcal{R}(\mathbb{T},\mathbb{C})$. The following formula holds: $$\dfrac{e_p(t,s;\mathbb{T})}{e_q(t,s;\mathbb{T})} = e_{p \ominus q}(t,s;\mathbb{T}),$$ where $e_p$ denotes the delta exponential and $\ominus$ denotes circle minus.
Proof
References
Theorem
If $q$ is continuous and $\mu$-regressive then $$e_q(t,s)=\hat{e}_{\frac{q^{\rho}}{1+q^{\rho}\nu}}(t,s)=\hat{e}_{\ominus_{\nu}(-q^{\rho})}(t,s),$$ where $e_q$ denotes the $\Delta$-exponential and $\hat{e}_q$ denotes the $\nabla$-exponential.
Proof
References
Theorem
If $q$ is continuous and $\mu$-regressive then $$e_q(t,s)=\hat{e}_{\frac{q^{\rho}}{1+q^{\rho}\nu}}(t,s)=\hat{e}_{\ominus_{\nu}(-q^{\rho})}(t,s),$$ where $e_q$ denotes the $\Delta$-exponential and $\hat{e}_q$ denotes the $\nabla$-exponential.
Proof
References
Theorem
If $p$ is continuous and $\nu$-regressive then $$\hat{e}_p(t,s)=e_{\frac{p^{\sigma}}{1-p^{\sigma}\nu}}(t,s)=e_{\ominus(-p^{\sigma})}(t,s),$$ where $\hat{e}_p$ denotes the $\nabla$-exponential and $e_p$ denotes the $\Delta$-exponential.
Proof
References
Examples
- The Gaussian bell
| $\mathbb{T}=$ | $e_p(t,s)=$ |
| $\mathbb{R}$ | $e_p(t,s)= \left\{ \begin{array}{ll} \exp \left( \displaystyle\int_s^t p(\tau) d \tau \right) &; t>s \\ 1 &; t=s \\ \exp \left( -\displaystyle\int_t^s p(\tau) d\tau \right) &; t<s \end{array} \right.$ |
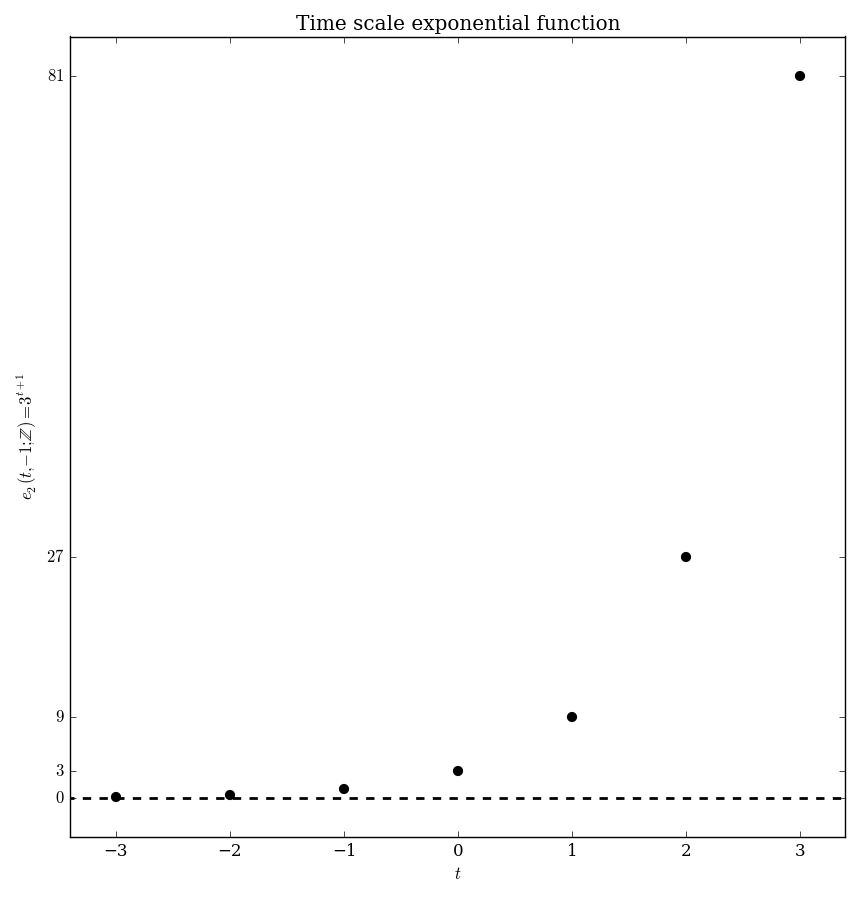
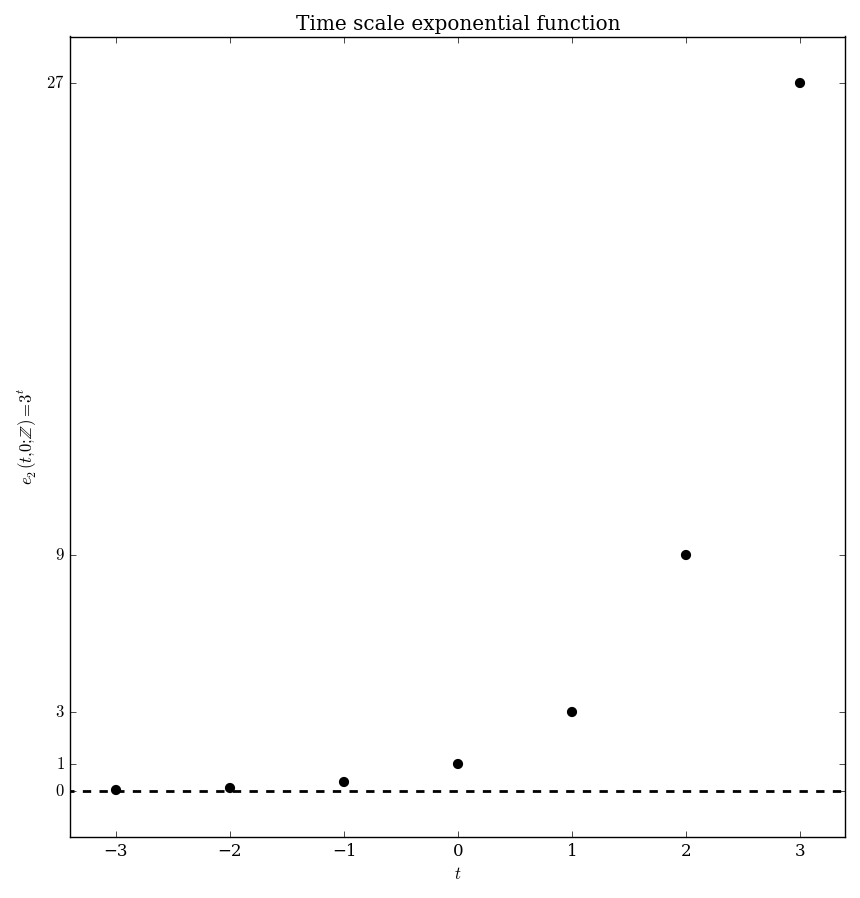
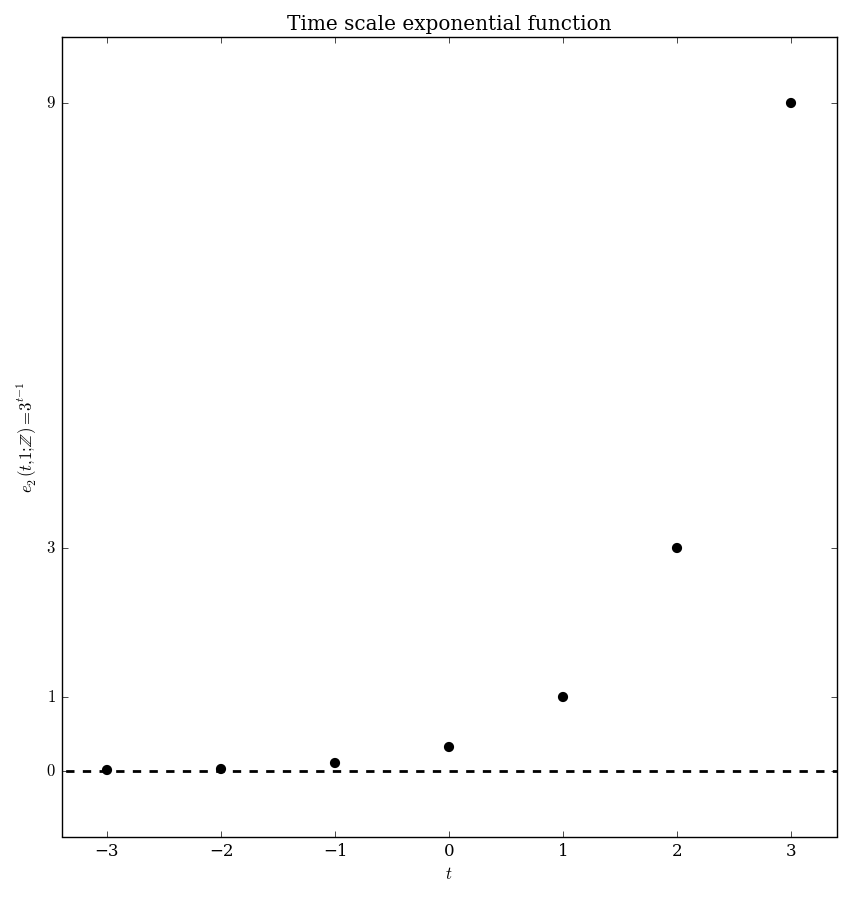
| $\mathbb{Z}$ | $e_p(t,s) = \left\{ \begin{array}{ll} \displaystyle\prod_{k=s}^{t-1} 1+p(k) &; t > s \\ 1 &; t=s \\ \displaystyle\prod_{k=t}^{s-1} \dfrac{1}{1+p(k)}&; t < s \end{array} \right.$ |
| $h\mathbb{Z}$ | $ e_p(t,s) = \left\{ \begin{array}{ll} \displaystyle\prod_{k=\frac{s}{h}}^{\frac{t}{h}-1} (1+hp(hk)) &; t > s \\ 1 &; t=s \\ \displaystyle\prod_{k=\frac{t}{h}}^{\frac{s}{h}-1} \dfrac{1}{1+hp(hk)} &; t < s \end{array} \right.$ |
| $\mathbb{Z}^2$ | $ e_p(t,s) = \left\{\begin{array}{ll} \displaystyle\prod_{k=\sqrt{s}}^{\sqrt{t}-1} 1 + p(k^2)(2k+1) &; t > s \\ 1 &; t=s\\ \displaystyle\prod_{k=\sqrt{t}}^{\sqrt{s}-1} \dfrac{1}{1+p(k^2)(2k+1)} &; t < s \end{array} \right.$ |
| $\overline{q^{\mathbb{Z}}}, q > 1$ | $e_p(t,s) = \left\{ \begin{array}{ll} \displaystyle\prod_{k=\log_q(s)}^{\log_q(t)-1} 1 + p(q^k)q^k(q-1) &; t > s \\ 1 &; t=s \\ \displaystyle\prod_{k=\log_q(t)}^{\log_q(s)-1} \dfrac{1}{1+p(q^k)q^k(q-1)} &; t < s \end{array} \right.$ |
| $\overline{q^{\mathbb{Z}}}, q < 1$ | $e_p(t,s) = \left\{ \begin{array}{ll} \displaystyle\prod_{k=\log_q(s)}^{\log_q(t)-1} 1 + p(q^k)q^{k-1}(1-q) &; t > s \\ 1 &; t=s \\ \displaystyle\prod_{k=\log_q(t)}^{\log_q(s)-1} \dfrac{1}{1+p(q^k)q^{k-1}(1-q)} &; t < s \end{array} \right.$ |
| $\mathbb{H}$ | $ e_p(t,s) = e_p\left( \displaystyle\sum_{k=1}^n \dfrac{1}{k}, \displaystyle\sum_{k=1}^m \dfrac{1}{k} \right) = \left\{\begin{array}{ll} \displaystyle\prod_{k=m}^{n-1} {1 + \dfrac{1}{k+1} p \left( \displaystyle\sum_{j=1}^k \dfrac{1}{j} \right)} &; t > s \\ 1 &; t=s \\ \displaystyle\prod_{k=n}^{m-1} \dfrac{1}{1 + \dfrac{1}{k+1} p \left( \displaystyle\sum_{j=1}^k \dfrac{1}{j} \right)} &; t < s \end{array} \right.$ |
See Also
$\Delta$-special functions on time scales | ||||||
$\cos_p$ |
$\cosh_p$ |
$e_p$ |
$g_k$ |
$h_k$ |
$\sin_p$ |
$\sinh_p$ |