Difference between revisions of "Delta sine"
From timescalewiki
(Created page with "{| class="wikitable" |+Time Scale Sine Functions |- |$\mathbb{T}$ | |- | $\mathbb{R}$ |$\sin_p(t,s)= $ |- | $\mathbb{Z}$ |$\sin_p(t,s) = \dfra...") |
|||
| (17 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | __NOTOC__ | |
| − | + | Let $\mathbb{T}$ be a [[time_scale | time scale]], let $s \in \mathbb{T}$, and let $\mu p^2 \colon \mathbb{T} \rightarrow \mathbb{R}$ be a [[regressive_function | regressive function]]. We define the trigonometric function $\sin_p \colon \mathbb{T} \times \mathbb{T} \rightarrow \mathbb{R}$ by | |
| − | + | $$\sin_p(t,s;\mathbb{T})=\dfrac{e_{ip}(t,s;\mathbb{T})-e_{-ip}(t,s;\mathbb{T})}{2i}$$ | |
| − | + | ||
| − | + | <div align="center"> | |
| − | + | <gallery> | |
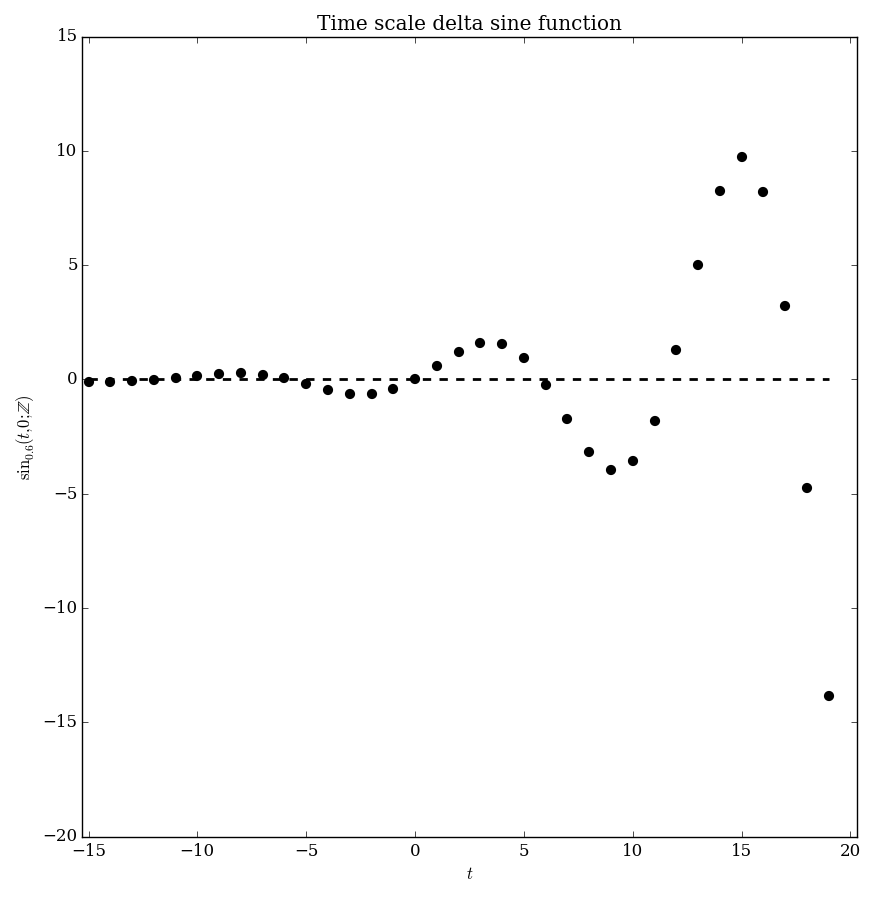
| − | + | File:Integerdeltasine,a=0.6,s=0plot.png | Plot of $\sin_{0.6}(t,0;\mathbb{Z})$. | |
| − | + | </gallery> | |
| − | + | </div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | | | + | =Properties= |
| − | + | [[Derivative of Delta sine]]<br /> | |
| − | + | [[Sum of squares of delta cosine and delta sine]]<br /> | |
| − | + | [[Derivative of delta cosine]]<br /> | |
| − | + | ||
| − | + | =Examples= | |
| − | + | {{:Table:Time scale delta sine functions}} | |
| − | + | ||
| − | + | <center>{{:Delta special functions footer}}</center> | |
| − | + | ||
| − | + | [[Category:specialfunction]] | |
| − | + | [[Category:Definition]] | |
| − | |||
| − | |||
| − | |||
Latest revision as of 14:13, 28 January 2023
Let $\mathbb{T}$ be a time scale, let $s \in \mathbb{T}$, and let $\mu p^2 \colon \mathbb{T} \rightarrow \mathbb{R}$ be a regressive function. We define the trigonometric function $\sin_p \colon \mathbb{T} \times \mathbb{T} \rightarrow \mathbb{R}$ by $$\sin_p(t,s;\mathbb{T})=\dfrac{e_{ip}(t,s;\mathbb{T})-e_{-ip}(t,s;\mathbb{T})}{2i}$$
Properties
Derivative of Delta sine
Sum of squares of delta cosine and delta sine
Derivative of delta cosine
Examples
| $\mathbb{T}$ | $\sin$$_p(t,s)= $ |
| $\mathbb{R}$ | |
| $\mathbb{Z}$ | $\dfrac{\displaystyle\prod_{k=t_0}^{t-1}1+ip(k) - \displaystyle\prod_{k=t_0}^{t-1}1-ip(k)}{2i}$ |
| $h\mathbb{Z}$ | |
| $\mathbb{Z}^2$ | |
| $\overline{q^{\mathbb{Z}}}, q > 1$ | |
| $\overline{q^{\mathbb{Z}}}, q < 1$ | |
| $\mathbb{H}$ |
$\Delta$-special functions on time scales | ||||||
$\cos_p$ |
$\cosh_p$ |
$e_p$ |
$g_k$ |
$h_k$ |
$\sin_p$ |
$\sinh_p$ |