Difference between revisions of "Delta sinh"
From timescalewiki
| (4 intermediate revisions by the same user not shown) | |||
| Line 9: | Line 9: | ||
=Properties= | =Properties= | ||
| − | + | [[Derivative of delta sinh]]<br /> | |
| − | + | [[Derivative of delta cosh]]<br /> | |
| − | + | [[Delta cosh minus delta sinh]]<br /> | |
| + | [[Delta hyperbolic trigonometric second order dynamic equation]]<br /> | ||
| − | + | <center>{{:Delta special functions footer}}</center> | |
| − | {{: | ||
| − | + | [[Category:specialfunction]] | |
| + | [[Category:Definition]] | ||
Latest revision as of 14:13, 28 January 2023
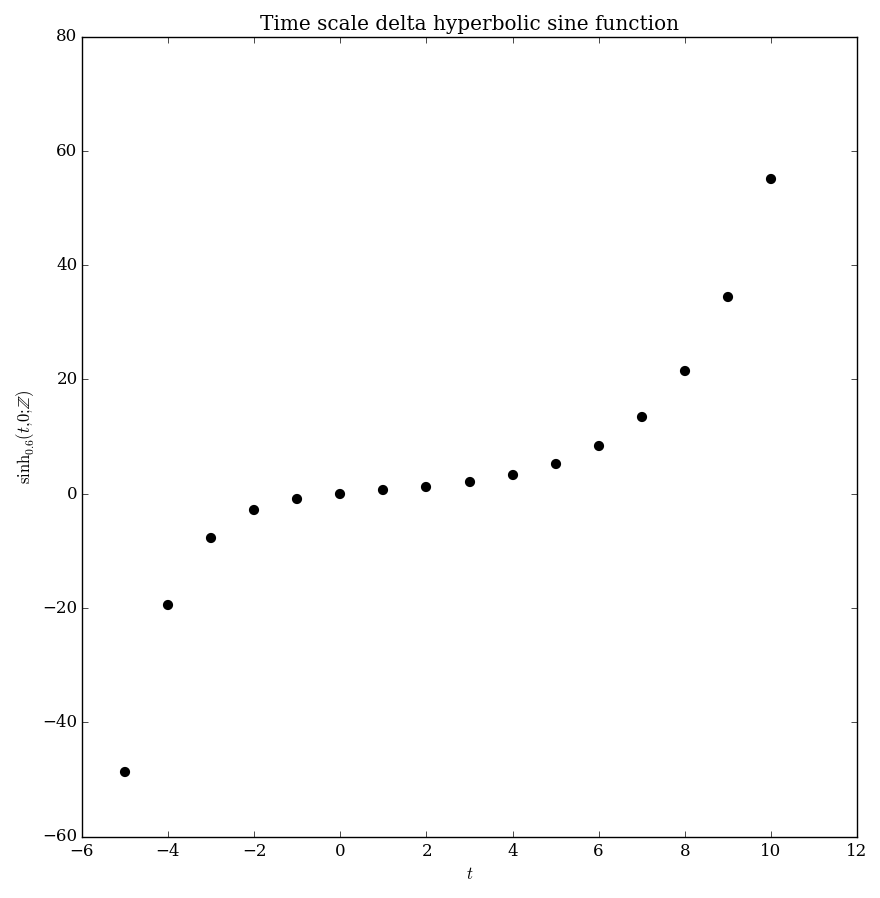
Let $p$ and $-\mu p^2$ be regressive functions. Then the $\Delta$ hyperbolic sine function is defined by $$\sinh_p(t,s) = \dfrac{e_p(t,s)-e_{-p}(t,s)}{2}.$$
Graph of $\sinh_{0.6}(t,0;\mathbb{Z})$.
Properties
Derivative of delta sinh
Derivative of delta cosh
Delta cosh minus delta sinh
Delta hyperbolic trigonometric second order dynamic equation
$\Delta$-special functions on time scales | ||||||
 $\cos_p$ |
 $\cosh_p$ |
 $e_p$ |
 $g_k$ |
 $h_k$ |
 $\sin_p$ |
 $\sinh_p$ |
