Multiples of integers
From timescalewiki
The set $h\mathbb{Z}=\{\ldots,-2h,-h,0,h,2h,\ldots\}$ of multiples of the integers is a time scale.
| Forward jump: | $\sigma(t)=t+h$ | derivation |
| Forward graininess: | $\mu(t)=h$ | derivation |
| Backward jump: | $\rho(t)=t-h$ | derivation |
| Backward graininess: | $\nu(t)=h$ | derivation |
| $\Delta$-derivative | $f^{\Delta}(t)=\dfrac{f(t+h)-f(t)}{h}$ | derivation |
| $\nabla$-derivative | $f^{\nabla}(t)=\dfrac{f(t)-f(t-h)}{h}$ | derivation |
| $\Delta$-integral | $\displaystyle\int_s^t f(\tau) \Delta \tau=$ | derivation |
| $\nabla$-integral | $\displaystyle\int_s^t f(\tau) \nabla \tau=$ | derivation |
| $h_k(t,s)$ | $h_k(t,s) = \dfrac{1}{k!} \displaystyle\prod_{\ell=0}^{k-1}(t-\ell h-s)$ | derivation |
| $\hat{h}_k(t,s)$ | $\hat{h}_k(t,s)=$ | derivation |
| $g_k(t,s)$ | $g_k(t,s)=$ | derivation |
| $\hat{g}_k(t,s)$ | $\hat{g}_k(t,s)=$ | derivation |
| $e_p(t,s)$ | $e_p(t,s)=\left\{ \begin{array}{ll} \displaystyle\prod_{k=\frac{t}{h}}^{\frac{s}{h}-1} \dfrac{1}{1+hp(hk)} &; t < s \\ 1 &; t=s \\ \displaystyle\prod_{k=\frac{s}{h}}^{\frac{t}{h}-1} 1+hp(hk) &; t>s. \end{array} \right.$ | derivation |
| $\hat{e}_p(t,s)$ | $\hat{e}_p(t,s)=\left\{ \begin{array}{ll} \displaystyle\prod_{k=\frac{t}{h}+1}^{\frac{s}{h}} (1-hp(hk)) &; t \lt s \\ 1 &; t=s \\ \displaystyle\prod_{k=\frac{s}{h}+1}^{\frac{t}{h}} \dfrac{1}{1-hp(hk)} &; t \gt s. \end{array} \right.$ | derivation |
| Gaussian bell | $\mathbf{E}(t)=\left[(1+h)^{\frac{1}{h}} \right]^{\frac{-t(t-h)}{2}}$ | derivation |
| $\mathrm{sin}_p(t,s)=$ | $\sin_p(t,s)=$ | derivation |
| $\mathrm{\sin}_1(t,s)$ | $\sin_1(t,s)=$ | derivation |
| $\widehat{\sin}_p(t,s)$ | $\widehat{\sin}_p(t,s)=$ | derivation |
| $\mathrm{\cos}_p(t,s)$ | $\cos_p(t,s)=$ | derivation |
| $\mathrm{\cos}_1(t,s)$ | $\cos_1(t,s)=$ | derivation |
| $\widehat{\cos}_p(t,s)$ | $\widehat{\cos}_p(t,s)=$ | derivation |
| $\sinh_p(t,s)$ | $\sinh_p(t,s)=$ | derivation |
| $\widehat{\sinh}_p(t,s)$ | $\widehat{\sinh}_p(t,s)=$ | derivation |
| $\cosh_p(t,s)$ | $\cosh_p(t,s)=$ | derivation |
| $\widehat{\cosh}_p(t,s)$ | $\widehat{\cosh}_p(t,s)=$ | derivation |
| Gamma function | $\Gamma_{h\mathbb{Z}}(t;s)=h\displaystyle\sum_{k=0}^{\infty} \left( \displaystyle\prod_{j=s}^{k-1} \dfrac{j+x}{j+1} \right) \dfrac{1}{(1+h)^{k+1}}$ | derivation |
| Euler-Cauchy logarithm | $L(t,s)=$ | derivation |
| Bohner logarithm | $L_p(t,s)=$ | derivation |
| Jackson logarithm | $\log_{h\mathbb{Z}} g(t)=$ | derivation |
| Mozyrska-Torres logarithm | $L_{h\mathbb{Z}}(t)=$ | derivation |
| Laplace transform | $\mathscr{L}_{h\mathbb{Z}}\{f\}(z;s)=$ | derivation |
| Hilger circle | 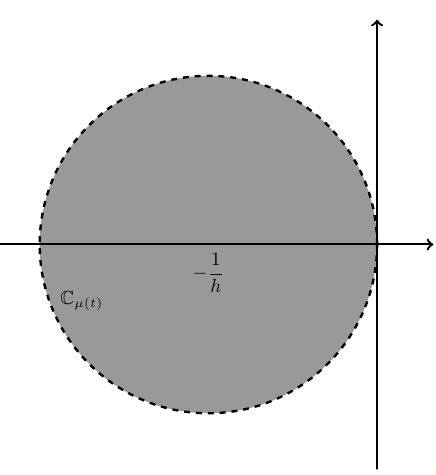
|
derivation |
References
Cauchy Functions and Taylor's Formula for Time Scales T
