Difference between revisions of "Delta sinh"
| Line 1: | Line 1: | ||
Let $p$ and $-\mu p^2$ be [[regressive function|regressive functions]]. Then the $\Delta$ hyperbolic sine function is defined by | Let $p$ and $-\mu p^2$ be [[regressive function|regressive functions]]. Then the $\Delta$ hyperbolic sine function is defined by | ||
$$\sinh_p(t,s) = \dfrac{e_p(t,s)-e_{-p}(t,s)}{2}.$$ | $$\sinh_p(t,s) = \dfrac{e_p(t,s)-e_{-p}(t,s)}{2}.$$ | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
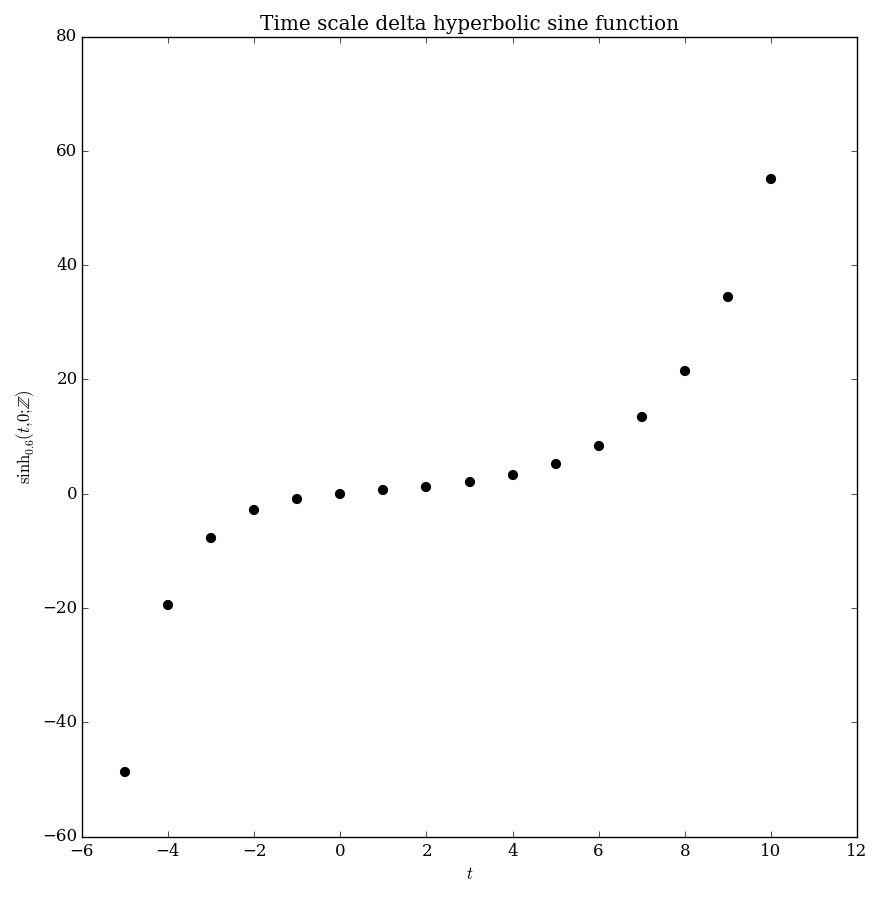
| + | File:Integerdeltasinh,a=0.6,s=0plot.png|Graph of $\sinh_{0.6}(t,0;\mathbb{Z})$. | ||
| + | </gallery> | ||
| + | </div> | ||
=Properties= | =Properties= | ||
Revision as of 08:02, 1 June 2016
Let $p$ and $-\mu p^2$ be regressive functions. Then the $\Delta$ hyperbolic sine function is defined by $$\sinh_p(t,s) = \dfrac{e_p(t,s)-e_{-p}(t,s)}{2}.$$
Contents
Properties
Theorem
Let $p\in$ $C_{rd}$. If $-\mu p^2 \in \mathcal{R}$, then $$\sinh^{\Delta}_p = p\cosh_p,$$ where $\sinh_p$ denotes the $\Delta$-$\sinh_p$ function and $\cosh_p$ denotes the $\Delta$-$\cosh_p$.
Proof
References
Theorem
The following formula holds: $$\cosh^2_p - \sinh^2_p = e_{-\mu p^2},$$ where $\cosh_p$ denotes the $\Delta$-$\cosh_p$ function, $\sinh_p$ denotes the $\Delta$-$\sinh_p$ function, and $e_p$ denotes the $\Delta$-$e_p$ function.
Proof
References
Theorem
Let $\gamma$ be a nonzero regressive real number, then a general solution of the second order dynamic equation is $$y^{\Delta \Delta}-\gamma^2 y= 0$$ is given by $$y(t) = c_1 \cosh_{\gamma}(t,s) + c_2 \sinh_{\gamma}(t,s).$$
Proof
References
Relation to other functions
Theorem
Let $p\in C_{rd}$. If $-\mu p^2 \in \mathcal{R}$, then $$\cosh^{\Delta}_p = p\sinh_p,$$ where $\cosh_p$ denotes the $\Delta$-$\cosh_p$ function and $\sinh_p$ denotes the $\Delta$-$\sinh_p$ function.
Proof
References
$\Delta$-special functions on time scales | ||||||
$\cos_p$ |
$\cosh_p$ |
$e_p$ |
$g_k$ |
$h_k$ |
$\sin_p$ |
$\sinh_p$ |